Perché in molti giochi ci sono cinque risorse?

Questa è una traduzione dell'articolo su Compound Interest, che potrete trovare a questo link.

Giocando a molti giochi da tavolo e di carte negli ultimi mesi, ho iniziato a notare una tendenza: la maggior parte dei giochi che contengono risorse, ne hanno cinque. Poiché essere in grado di contare tutti i colori da una parte non sembrava una ragione sufficiente, ho iniziato a cercare se ci fosse un significato più profondo dietro quello che sembra essere quasi uno standard del settore (quasi sempre rappresentato di cinque colori, quindi userò "colori" e "risorse" in modo intercambiabile in questo articolo).

I giochi

Prima di scavare a fondo, ho deciso di concentrarmi su tre dei miei giochi preferiti che seguivano tutti questa regola. Probabilmente ci sono molti altri giochi che si adattano a questo schema, ma questi saranno ciò su cui mi concentrerò adesso. Dai un'occhiata alle pagine pertinenti se vuoi saperne di più su, ma ho incluso un sommario super succinto delle loro regole e di come usano le risorse, sotto ciascuna di esse.

Catan (Conosciuto come I Coloni di Catan)

Le cinque risorse: mattoni, legname, lana, grano e minerale.

In Catan raccogli risorse ogni turno (se il tiro di dado ti è benevolo), poi userai una combinazione di queste risorse per costruire varie cose (strade, insediamenti, città e carte sviluppo). Questi, valgono punti e la prima persona che ne raggiunge dieci vince, essenzialmente cercherai di raccogliere la giusta combinazione di risorse più rapidamente dei tuoi avversari.

Splendor

Le cinque gemme: smeraldo, diamante, zaffiro, onice e rubino. L'oro è effettivamente un jolly, piuttosto che il colore rappresentato.

In Splendor, passerai il tuo turno a raccogliere gemme o spendendole in carte che ti daranno una combinazione di punti e gemme riutilizzabili. C'è una riserva limitata di gemme e ogni giocatore può tenerne solo dieci alla volta; il tuo obiettivo è di arrivare a quindici punti, prima prendendo e conservando strategicamente le gemme, poi usandole per acquistare più carte che velocizzeranno il tuo potere d'acquisto.

Magic: The Gathering

I cinque mana: bianco, blu, nero, rosso e verde.

In Magic, le risorse sono disponibili in cinque colori diversi e giochi carte di uno o più colori per attaccare i tuoi avversari e portarli a zero punti. Alcune carte forniscono risorse e altre usano quelle risorse per produrre effetti che ti aiutano o danneggiano il tuo avversario. A differenza degli altri due giochi, componi in anticipo il tuo mazzo (di sessanta carte) includendo un singolo colore o qualsiasi combinazione dei cinque. I vari colori interagiscono in modi interessanti, con alcuni mazzi che hanno vantaggi rispetto ad altri, come un gioco incredibilmente complicato di Sasso-Carta-Forbici con al suo interno molta più abilità. 

Usano tutti le risorse in modo molto diverso, ma ciò che hanno in comune è che ce ne sono cinque, con Magic e Splendor che scelgono persino gli stessi colori: bianco, nero, blu, rosso e verde. Dal momento che ha la base di fan più grande e nerd (me compreso), ci sono state alcune buone discussioni sul motivo per cui Magic abbia cinque colori , ma ero curioso di vedere se ci fossero ragioni alla base dietro a ogni gioco che fa la stessa scelta.

Il gameplay

Il mio primo pensiero è stato che la ragione principale deve essere l'equilibrio: gli autori vogliono sempre bilanciare le risorse in modo che nessuna sia troppo dominante, altrimenti le persone giocherebbero sempre la strategia "migliore" o si concentrerebbero esclusivamente sulla raccolta della risorsa "migliore", diventando noiosa velocemente. Tre strategie, come in Sasso-Carta-Forbici, sono perfettamente bilanciate ma non molto interessanti. Con quattro o cinque opzioni, ci sono molte più interazioni uno contro uno, ma non una quantità enorme come quando raggiungi sei o sette. Se rappresentato visivamente, è chiaro quanto le cose si complichino all'aumentare del numero di punti:

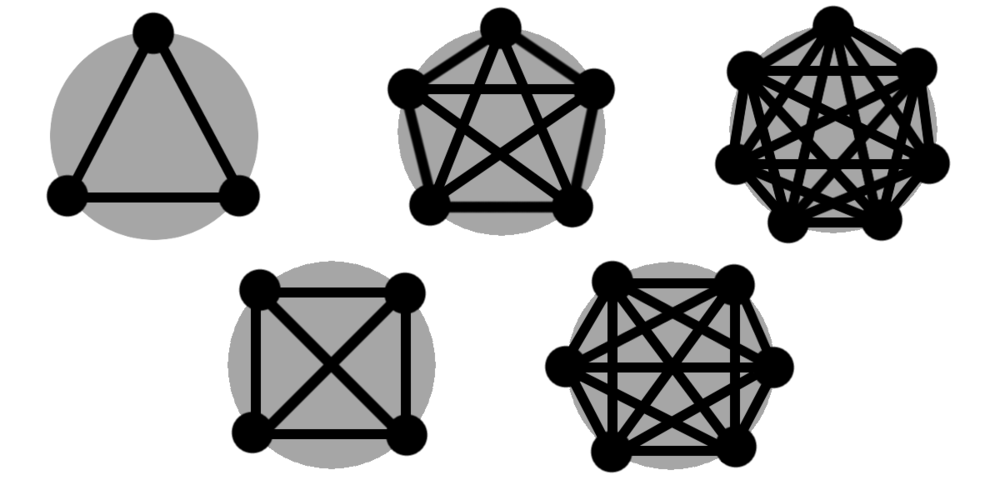
Ogni punto aggiuntivo aggiunge più connessioni 1:1 rispetto al punto precedente. Bilanciare un gioco a sette risorse è il doppio più complicato che bilanciare un gioco a cinque risorse.

È stato un inizio, ma tra questi tre giochi, Magic è l'unico in cui puoi giocare con successo una strategia a risorsa singola. In Catan, tutto ciò che puoi costruire richiede almeno due risorse e alcuni ne usano tre o quattro. In Splendor, le carte possono usare da una a quattro delle gemme e non puoi evitare di pescare gemme di più colori. E mentre puoi giocare a Magic con un mazzo monocolore, la gioia centrale del gioco sta nell'usare più colori in un mazzo per combinarne le strategie e abilità.

Le carte Splendor costano gemme e il prezzo (in basso a sinistra di ogni carta) può includere multipli di una gemma o combinazioni di più gemme.

A Catan, se raccogliessi solo una risorsa, non saresti mai in grado di costruire nulla.

Molte carte di Magic richiedono più di un colore di mana, come questa carta che richiede sia il blu che il rosso.

Poiché le interazioni dei colori sono così importanti, gli autori devono anche considerare il numero di combinazioni possibili e se limitarle in qualche modo. Poiché Catan è progettato per essere molto semplice, ci sono solo quattro combinazioni: due che coinvolgono due risorse, una che coinvolge tre risorse e una che coinvolge quattro risorse. Questo rende il gioco accessibile ai principianti e generalmente richiede ai giocatori di utilizzare tutte le risorse (poiché alcune carte sviluppo ti permettono di costruire strade, è possibile vincere senza usare argilla, ma è molto difficile da ottenere).

All'estremo limite della complessità, Magic consente ogni possibile combinazione di colori, da carte e mazzi monocolore, a quelli che utilizzano due, tre, quattro o tutti e cinque i colori. Quando questa gamma completa d'interazioni è consentita, il numero di combinazioni aumenta rapidamente e ha iniziato a richiedere un po' più di calcoli matematici di quanto potessi fare con la mia testa.

I calcoli matematici

Per vedere quante combinazioni sarebbero possibili con diversi numeri di risorse, ho creato questa tabella (con l'aiuto di questo pratico calcolatore online per i numeri più grandi):

Le combinazioni di due colori sono le più semplici e con cinque colori si ottengono dieci coppie possibili. Ci sono solo sei accoppiamenti quando hai quattro colori e quindici quando ne hai sei. Con sette colori hai ventuno abbinamenti, più del doppio del numero di abbinamenti con cinque colori. Andando oltre, diventa così complicato che sarebbe difficile da gestire per gli autori (figuriamoci per i giocatori).

Tutti questi giochi includono combinazioni di tre colori, che potrebbero rendere le cose ancora più complicate... ma con cinque colori, il numero di combinazioni da tre è uguale al numero di combinazioni di due colori: dieci. Ciò ha senso intuitivo, poiché una combinazione di due colori è in realtà solo l'esclusione degli altri tre colori. 

Magic ha nomi per ciascuna delle possibili combinazioni di colori e, limitare il numero massimo di combinazioni a dieci, rende questo compito molto più semplice.

Se ci fossero sette colori con trentacinque possibili combinazioni di tre colori, questo semplice grafico non sarebbe possibile. Credito dell'immagine .

Ma quando vai fino a sei colori, ci sono venti combinazioni di tre colori, il doppio del numero più alto di combinazioni con solo cinque colori. Per sette colori, il numero di combinazioni di tre colori salta a trentacinque. Che si tratti del numero di edifici a Catan o di carte in Splendor o Magic, trentacinque combinazioni rappresenterebbero un numero enorme di opzioni. 

Guardando questa tabella, ho notato che ogni colonna era simmetrica, ad esempio sei colori includono una sequenza di 6/15/20/15/6. Dato che questo era uno schema che ho notato dopo aver fatto un po' di conti, ero sicuro che qualcuno avesse già un nome per questo, e alcune veloci ricerche su Google mi hanno mostrato che avevo ragione. 

Questa tabella è essenzialmente il "coefficiente binomiale", che è il gergo matematico per "combinazioni di due numeri". Il coefficiente binomiale può anche essere rappresentato da qualcosa chiamato Triangolo di Pascal, una piramide di numeri in cui ogni numero è la somma dei due numeri direttamente sopra di esso. Vedere questo mi ha fatto tornare indietro a un libro di testo di matematica delle scuole superiori dimenticato da tempo:

Triangolo di Pascal.

Come si può vedere, questi sono gli stessi numeri della mia tabella qui sopra, con ogni riga che rappresenta un certo numero di colori e ogni riga che elenca il numero di connessioni a 0, 1, 2, 3, eccetera possibili. Ancora una volta, andare oltre i cinque numeri (la sesta riga nel triangolo di Pascal) accelera drasticamente la complessità.

Vale anche la pena considerare il numero totale di combinazioni (l'ultima colonna della mia tabella) e, ancora una volta, cinque risorse sembrano una buona media. Ogni volta più o meno raddoppia, con cinque colori per un totale di trentuno combinazioni. Si può avere un gioco solido a quattro colori con quindici combinazioni, o un gioco a sei colori più complicato con sessantatre combinazioni, ma arrivare fino a un gioco a sette colori con centoventisette combinazioni possibili sembra troppo da gestire per il cervello umano (per lo meno divertendosi). 

Non ci sono verità universali e sono sicuro che i giocatori più occasionali apprezzerebbero giochi con tre o quattro risorse, mentre i giocatori più assidui apprezzerebbero quelli con sei o più, ma poiché i giochi di maggior successo cercano di accontentare sia i giocatori occasionali che quelli assidui (qualcosa chiamato "design lenticolare " una filosofia di progettazione coniata da Mark Rosewater, il lead designer di MTG, che si riferisce alle carte di Magic come "sembrano essere molto semplici, ma una volta che hai capito di più su come usarle, diventano più complesse"), cinque risorse sembrano essere il modo migliore per raggiungere quell'equilibrio.

Le conclusioni

Spero che questa immersione nella matematica all'interno del design dei giochi da tavolo vi sia piaciuta tanto quanto me. Ovviamente c'è ancora molto da analizzare e spero di addentrarmi ancora più a fondo al più presto. 

Ammetto anche che ci sono molti giochi che non si adattano a questo modello. Per me, la più notevole è la serie Civilization, con Civilization VI che ha sette o otto risorse, a seconda di come le conti, ma quel livello di complessità funziona davvero solo per i giochi da computer in cui una macchina esegue tutto il calcolo e il monitoraggio per te. I giochi da tavolo, in cui gli umani si occupano di mescolare i mazzi e di tenere conto delle transazioni, generalmente devono essere più semplici per essere divertenti.

Cinque sembrano essere un numero perfetto di risorse per tutti questi motivi: bilanciare strategie, facilità di progettazione e piacere ai giocatori occasionali e scafati. Se conoscete altri giochi che si adattano a questo stampo, o che invalidano la mia teoria, mi piacerebbe saperne di più, quindi fatemelo sapere.