Una parte essenziale del divertimento nei giochi consiste ne non sapere cosa aspettarsi. Suspense, sorpresa, decisioni difficili sono cose che cerchiamo quando giochiamo. E per far sì che un gioco resti divertente, ogni partita deve essere diversa dall’ultima.
Qui vedremo come i giochi possano rendere unica ogni partita e come questo obiettivo sia ottenuto da un gioco in particolare: Flamme Rouge, un gioco di corse di ciclismo professionistico.
Non c’è niente di unico nella rigiocabilità di Flamme Rouge, ma dal momento che questo post è venuto fuori da quello del gioco da tavolo modulare su cui stavo lavorando, è perfetto per introdurre l’argomento!
Se non conosci Flamme Rouge, puoi leggere la mia recensione e un riassunto di come si gioca qui: Analyzing Flamme Rouge.
In un articolo successivo, aggiungerò un’esplorazione approfondita di una particolare fonte della variabilità del gioco: la plancia modulare di Flamme Rouge.
E siccome è divertente prendere sul serio domande leggere, farò del mio meglio per arrivare ai veri numeri utili a descrivere quante combinazioni uniche del tabellone di gioco siano possibili in Flamme Rouge.
Ma per ora, diamo un’occhiata alle variabili di gioco.
Esistono diversi modi per aggiungere imprevedibilità a un gioco e non tutti implicano lanciare dadi o pescare carte.
Meccanismi basati sulla fortuna
Ecco tre modi di aggiungere imprevedibilità che coinvolgono una qualche forma di fortuna:
usare meccaniche basate sulla fortuna, come pescare da un mazzo di carte o tirare un dado;
nascondere le informazioni ai giocatori (dove i giocatori devono prendere decisioni sulla base di informazioni parziali);
fare in modo che i giocatori prendano decisioni contemporaneamente (come carta-sasso-forbici).
Tutte queste meccaniche richiedono al giocatore di prendere decisioni basate su informazioni parziali.
Il meglio che tu possa fare in questo caso è fare affidamento su una previsione dei risultato, com’è necessario fare quando sono coinvolte la fortuna o, se preferisci, le probabilità.
Sembrerebbe che io non sia il primo a pensarlo, dato che ho scoperto da poco che qualcuno ci ha tirato anche fuori un gioco: Princess Bride: The Batte of Wits.
Un’ultima cosa da annotare: quando sono coinvolti meccanismi basati sulla fortuna, a volte quanto più spesso un evento si ripete minore sarà la fortuna a determinare chi sia il vincitore finale.
Facciamo un esempio: il lancio di una monetina bilanciata. [NdT: "Toss a fair/unfair coin" è qui sempre reso come bilanciata/sbilanciata, con significato ulteriore di giusto/ingiusto]
Il caso di un evento singolo
Se tutto dipende dal singolo lancio di una moneta, hai un 50-50 di chances di vittoria. Questo esempio è molto dipendente dalla fortuna.
Il caso di un evento ripetuto 1000 volte
Se ci sono 1000 lanci di una moneta, se non si prende in considerazione altro e il vincitore è determinato semplicemente da chi ne vince la maggioranza, continui ad avere un 50-50 di possibilità di vittoria.
Sebbene questo possa aumentare un po’ la suspense, sapere che non si può fare altro per cambiare il risultato renderà in genere solo il processo più tedioso.
In ogni caso, cosa accadrebbe nel caso la monetina non fosse bilanciata?
The unfair twist ("monetina non bilanciata")
Diciamo che in qualche modo sei in grado di ottenere un piccolo vantaggio. In una partita questo potrebbe semplicemente significare che sei più bravo a pianificare o che hai trovato un una buona combinazione di mosse da usare. Se in qualche modo riesci ad aumentare le tue possibilità di vincita dell’1%, rendendolo un lancio di moneta sbilanciato con il 51% contro il 49%, questo può alterare drasticamente le prospettive del gioco.
Un lancio di una moneta non bilanciata
Se un solo lancio di moneta determina l’esito della partita, le tue possibilità sono pressoché invariate: 51% a 49%. Non molto meglio di un 50-50 di probabilità, quindi il risultato sarà ancora in gran parte determinato dalla fortuna.
Mille lanci di una moneta non bilanciata
Tuttavia per 1000 lanci di moneta dovresti arrivarne a vincerne circa 510, perdendone i restanti 490. Se il gioco dipende dall’avere la maggioranza delle vittorie le possibilità del tuo avversario diminuiscono drasticamente.
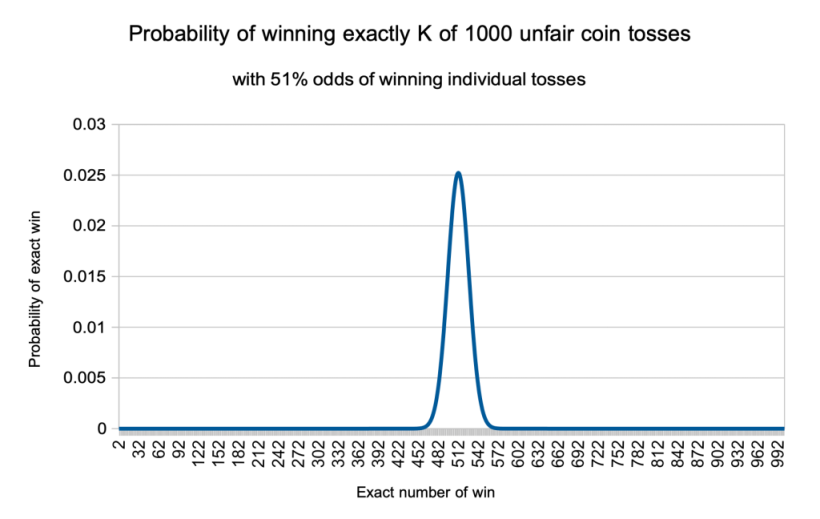
Per numeri grandi come 1000, le probabilità di vincere un numero specifico di eventi tendono a concentrarsi intorno al numero 510, il numero di vincite previsto, con circa il 2,5% di possibilità di vincere esattamente 510 volte. Basta dare un’occhiata alla probabilità di ottenere un numero specifico di vincita e vedere quanto sono raggruppate le probabilità attorno ai risultati attesi:
Per 1000 lanci questa differenza dell’1% genera in realtà una probabilità del 75% di vincere la maggior parte dei lanci. Un aumento del 2% porta al 90% la possibilità di vittoria.
Per questo calcolo ho usato una cosa chiamata “distribuzione binomiale”, un tipo di calcolo disponibile nel tuo programma di fogli di calcolo preferito.
Per i curiosi di matematica
Viene calcolata utilizzando le seguenti informazioni: la probabilità di vincita è P(win), la probabilità di sconfitta è P(losing) (raffigurata qui come 1-P(win), il numero di lanci: N, il numero esatto di vittorie K.
Tradotto: il numero di possibili modi in cui può verificarsi un numero specifico di vincite, moltiplicato per la probabilità effettiva che si verifichi questo numero effettivo di vincite.
Per una singola vincita si darà: Dato che la vincita può verificarsi al primo lancio, o al secondo, fino all'ultimo si pone 1000 moltiplicato per la probabilità di vincere una volta (0,51) moltiplicato 999 volte con la probabilità di perdere, o anche (0.49)999.
Per sapere quali sono le tue possibilità di vincerne la maggior parte, devi semplicemente ricalcolare questo per tutti i numeri di K in cui vinci (501,502,503, ecc…), e sommare le probabilità individuali per ottenere la possibilità complessiva di vincita!
E per un normale gioco da tavolo?
Ovviamente, pochi giochi da tavolo consistono nel lancio di monete. Ma potresti seguire lo stesso identico ragionamento, usando calcoli solo leggermente più complicati, per qualsiasi evento basato sulla probabilità in un gioco da tavolo.
In un tipico gioco da tavolo probabilmente non si assisterà a migliaia di eventi, ma anche con un più ragionevole numero di 100 eventi in un solo gioco, considera questo:
una probabilità del 51% di vincere un singolo evento si traduce in una probabilità del 62% di vincere la partita;
una probabilità del 52% su un singolo evento si traduce in una probabilità del 69% di vincere la partita;
una probabilità del 60% ti porterà al 98% di possibilità di vincere la partita.
Quindi le probabilità aumentano lentamente, ma la ripetizione elimina sicuramente la fortuna dall'equazione!
Maggiore è il numero di eventi, più facile sarà prevedere i risultati.
O meglio:
Più alto è il numero di eventi, più le capacità del giocatore vengono prese in considerazione e meno si finisce per dipendere dal tradizionale concetto di fortuna.
Ma se nessun tipo di fortuna è “your cup of tea”, altri modi per aggiungere variazioni tra una partita e l’altra possono venire dal gioco stesso.
Variazioni non basate sulla fortuna
Ecco tre modi per aggiungere variazioni non basate sulla fortuna in un gioco:
avere un numero molto elevato di possibili stati di gioco (come negli scacchi o anche in go);
consentire regole o variabilità del potere dei giocatori (come offrire diverse fazioni con diverse capacità tra cui scegliere);
avere una varietà di impostazioni di gioco iniziali... come avere un gioco da tavolo modulare!
Uno spazio di stato molto ampio è un bel modo per fornire variabilità. Negli scacchi e in go le regole e il tabellone sono statici, la configurazione iniziale è sempre la stessa e non ci sono informazioni nascoste, eppure esse forniscono così tante scelte ad ogni passaggio, che è possibile che non ci saranno mai due partite giocate allo stesso modo! Un avvertimento per il giocatore occasionale è che le abilità del giocatore diventano quindi il tratto distintivo per questo tipo di giochi. (Si potrebbe obiettare che c'è un po' di fortuna nella selezione delle mosse impossibile da prevedere completamente, ma questo non è un argomento molto forte!).
Fornire diverse fazioni o variazioni nei poteri a disposizione di un giocatore durante una partita consente una maggiore variabilità, la cui quantità dipenderà dal numero di fazioni disponibili o variabili tra cui scegliere. Di solito mi piacciono molto i giochi con più fazioni poiché ogni fazione spesso fornisce un'esperienza di gioco completamente diversa, ma ciò presenta un possibile svantaggio: i problemi di bilanciamento.
Per i giocatori dedicati, le fazioni offrono l'opportunità di trovare casi particolari che rischiano di “rompere” il gioco se offrono un vantaggio troppo grande. Questo è in ogni caso un argomento a parte già di per sé ed è generalmente relativo allo specifico gioco…
Infine, i giochi da tavolo modulari, consentono giochi in continua evoluzione, senza influire sulla difficoltà del gioco e senza dover imparare nuove regole! Si tratta di un meccanismo molto popolare, utilizzato da famosi giochi da tavolo come Catan, ma anche Forbidden Island, Betrayal at the house on the Hill, Takenoko e molti altri. Ecco un elenco esaustivo di giochi da tavolo modulari da Board Game Geek.
Un gioco può utilizzare alcuni o tutti questi meccanismi, dalla variabilità del gioco all'imprevedibilità, per rendere ogni gioco diverso.
Ciò influenzerà evidentemente quanto può essere diverso un gioco dall'altro. Ma forse più significativamente, quegli elementi di variabilità determineranno qual è l'importanza dell’abilità dei singoli giocatori nel determinare il vincitore.
Cercare di determinare qual è la parte della fortuna e la parte delle abilità in un gioco è una domanda non banale. Una di quelle che mi ha ispirato ad aprire questo blog. Ma sono ben lungi dall'averlo affrontato seriamente, dato che è praticamente la tana del bianconiglio!
Detto ciò… Volevo avere uno sguardo pratico su tutto questo. Quindi diamo un'occhiata a Flamme Rouge e vediamo come il gioco implementa la variabilità attraverso la lente dei meccanismi di cui sopra.
In Flamme Rouge, ogni giocatore controlla due ciclisti, ciascuno con il proprio mazzo di 15 carte. Il valore delle carte rappresenta di quanti spazi avanza un ciclista quando ne viene giocata una.
Ecco i valori specifici per ogni mazzo:
Per il Rouleur (in italiano passista), 3 carte per ognuno dei seguenti valori: 3-4-5-6-7
Per lo Sprinteur (in italiano velocista), 3 carte per ognuno dei seguenti valori: 2-3-4-5-9
Durante il gioco, ogni volta che un ciclista si trova a tirare davanti un gruppo di ciclisti, il suo mazzo verrà arricchito da una carta di basso valore, giustamente chiamata “carta fatica”.
Giocando simultaneamente, ogni turno, i giocatori pescano quattro carte a caso per uno dei loro ciclisti e selezionano segretamente una carta da giocare. Quindi ripetono questo processo per il secondo ciclista, usando il secondo mazzo di carte.
La pesca delle carte
Le 4 carte che peschi per il tuo ciclista determinano cosa puoi giocare in un turno. Questo ha il potenziale per limitarti in alcuni momenti cruciali del gioco.
La selezione sequenziale delle carte
Poiché devi selezionare la carta per un ciclista PRIMA di vedere le 4 possibili carte da giocare per il tuo secondo ciclista, sei limitato nell'efficacia con cui puoi coordinarti tra i tuoi ciclisti.
Per essere espliciti: questo è ciò che ho chiamato informazioni nascosta: Quando selezioni la carta per il primo ciclista, non sai quali saranno le 4 possibili scelte per il tuo secondo ciclista.
È relativamente facile tenere mentalmente traccia di ciò che è rimasto nei tuoi mazzi. E se non hai troppe carte fatica, avrai una buona idea delle carte che dovresti essere in grado di giocare durante il tuo prossimo turno. Sarei disposto a giocare a questo gioco senza l'elemento della pesca. Credo che la semplice selezione delle carte da giocare ogni turno da ogni mazzo probabilmente non modificherebbe troppo il gioco e penso sarebbe altrettanto divertente!
Fonti minori e maggiori
Poiché i mazzi sono relativamente piccoli e hanno sempre la stessa composizione iniziale, gli elementi di pesca delle carte e selezione sequenziale aggiungono qualche variazione al gioco, ma non sono il principale fattore di imprevedibilità. Certo, spesso può influenzare l'esito di una corsa, ma un buon giocatore giocherà ogni mazzo per ridurre al minimo quelle incognite.
Simulazione simultanea
In Flamme Rouge, tutti i giocatori selezionano le proprie carte contemporaneamente e aspettano che tutti siano pronti prima di rivelare le proprie carte.
A mio parere, la più grande fonte di imprevedibilità in questo gioco deriva da questa selezione simultanea di carte da parte dei giocatori. Le decisioni prese da altri sono ciò che influenza realmente lo svolgimento della gara e non è un elemento neutrale di imprevedibilità.
Se questo fosse un fenomeno casuale, potremmo aspettarci che la selezione simultanea colpisca tutti i giocatori allo stesso modo. Ma ci sono certamente alcune abilità delle persone in gioco quando si cerca di prevedere come gli altri sceglieranno le loro carte...
In questo risiedono alcune fonti di casualità basata sull’alea in questo gioco.
Ci sono principalmente 3 diversi meccanismi di interazione integrati nel gioco.
Lo slip streaming (o scia), l'atto di utilizzare altri ciclisti davanti a te per avanzare senza alcun costo, se lasci uno spazio tra te e loro.
Il blocco, accidentale o programmato. C'è spazio solo per 2 ciclisti affiancati. Hai bisogno di abbastanza movimento per essere in grado di andare avanti di loro, o rimarrai bloccato dietro di loro mentre avanzi.
Fatica. Qualsiasi ciclista che finisce davanti a un gruppo e non è in grado di scivolare dietro un altro gruppo, dovrà aggiungere una carta fatica al proprio mazzo, quindi i giocatori possono provare a rimanere indietro per evitare di accumulare troppe carte fatica.
Durante una gara, pensare al futuro e cercare di ridurre al minimo gli effetti negativi sui tuoi ciclisti, migliorando al contempo le tue possibilità di beneficiare della scia (o negarla agli altri) è il punto cruciale del gioco. Qualcosa che può richiedere alcune giocate per comprendere appieno!
Quindi il gioco simultaneo è dove penso sia la fonte più significativa di incertezza, gli altri sono semplicemente meccanismi di interferenza per le strategie del giocatore. È un meccanismo divertente, perché pone l'interazione del giocatore al centro del gioco e ha l'ulteriore vantaggio di accelerare un po' il gioco rispetto a un approccio più basato sui turni!
E il numero di eventi, quindi?
Nota: prima di procedere con questa spiegazione specifica sulla significatività statistica, vorrei sottolineare che non sono un esperto di statistica. Sembrava avere senso parlarne un po', data la discussione sul lancio della moneta in precedenza in questo post. Quindi prendi quanto segue con le pinze e, per favore, fammi sapere se ti capita di essere un esperto con conoscenze più approfondite.
Come ho spiegato in precedenza con l'esempio del lancio della moneta, la ripetizione è ciò che consente all’abilità del giocatore di brillare.
In Flamme Rouge, potremmo dire che ci sono circa 15 turni in una corsa, spesso un po' meno, in cui ogni giocatore pesca ogni volta da 2 mazzi. Quindi potremmo dire circa 30 eventi di estrazione e selezione di una carta. 30 decisioni da prendere che interagiranno per decidere chi sarà il vincitore.
Un fattore importante nel mio esempio di lancio della moneta era che gli eventi erano indipendenti. Ogni lancio della moneta non è in alcun modo influenzato dai precedenti risultati del lancio della moneta. Quindi l'ordine delle vittorie non ha importanza.
Questo non sarebbe il caso, ad esempio, di Catan, o Monopoly, o anche degli scacchi, dove un vantaggio iniziale tende ad amplificarsi durante il gioco a causa dell'effetto composto (più risorse all'inizio ti consentono di acquistare più risorse producendo cose prima, o un vantaggio strategico ti consente ulteriori guadagni più avanti nel gioco).
Direi che i turni di Flamme Rouge sono più o meno indipendenti, dato che ogni turno che giochi, il tuo ciclista ha la possibilità di vincere o perdere qualche spazio rispetto alla carta che è stata giocata. Poiché la somma dei valori delle carte in un mazzo è uguale per tutti, e prossima alla distanza totale da percorrere in una gara, la “vincita” non avviene giocando una carta di valore superiore, ma beneficiando di slip streaming o nel bloccare altri, eventi che si traducono nell'aumentare o diminuire la distanza che puoi effettivamente percorrere con il tuo mazzo.
I risultati si accumulano verso la vittoria finale, ma gli effetti non vengono amplificati nel tempo. Sto allargando un po' qui l'applicazione del campionamento, ma quando vengono campionati eventi casuali e indipendenti, 30 eventi sono spesso sufficienti per dare una misura accurata dei fenomeni sottostanti, con un ragionevole margine di errore. Nei sondaggi, fanno la stessa cosa. Potresti avere familiarità con avvertimenti come: entro 3,1 punti percentuali 19 volte su 20, che mette in numero la probabilità che i numeri che ti hanno appena dato siano rappresentativi dell'opinione reale dell'intera popolazione. Il che ti dà comunque una probabilità del 5% di avere sfortuna quando selezioni casualmente un campione e finisci con un gruppo di persone non rappresentativo che ti dà la loro opinione (supponendo che il campionamento casuale sia fatto correttamente)!
Nel nostro caso, supponiamo che stiamo cercando di misurare chi è il miglior giocatore del gioco. La mia conoscenza rudimentale qui mi dice che 30 campioni sono abbastanza sufficienti perché una misura abbia un significato. C'è una certa casualità nel gioco, ma se le abilità del giocatore non corrispondono, questo dovrebbe essere sufficiente per inclinare la bilancia in modo statisticamente significativo, e quindi misurabile, verso il giocatore migliore!
Sfortunatamente, questa affermazione non è indipendente dalla mia personale comprensione di Flamme Rouge, quindi è un po' come barare! Avere accesso a poche migliaia di giochi giocati su un'app Flamme Rouge da centinaia di giocatori sarebbe probabilmente un approccio migliore per determinare il fattore abilità nel gioco!
Nella mia situazione limitata, dovrò esplorare un po' questo aspetto prima di poterti dare una risposta più scientifica! Spero di ottenere alcuni dati sperimentali quando tento di scrivere una guida strategica che includa alcune simulazioni di gioco. Ma nel frattempo, sentiti libero di partecipare se hai buone intuizioni da condividere con me e gli altri!
Esaminiamo la fonte di imprevedibilità non basata sulla fortuna
In Flamme Rouge, c'è una parte che aggiunge un'enorme variabilità da un gioco all'altro senza influire sulle possibilità di vittoria dei singoli giocatori: il tabellone stesso!
La pista della corsa, con tutte le sue colline e pendii, è costruita con parti di pista, rendendo Flamme Rouge un gioco da tavolo modulare! Il gioco include 6 esempi di piste da corsa, ma il numero potenziale di diverse piste che puoi costruire è enorme!
Avere un tabellone modulare aggiunge una grande capacità di rigiocabilità, senza nascondere alcuna informazione ai giocatori. Certo, alcune tracce consentiranno ai giocatori più abili di eclissare i loro coetanei più facilmente, ma almeno lo fa in modo trasparente.
Si potrebbe dire che a causa delle interazioni dei giocatori e delle informazioni nascoste, ogni corsa in Flamme Rouge ha il potenziale per essere comunque diversa. Ma correre sempre sulla stessa pista potrebbe diventare abbastanza ripetitivo. Per questo credo che l'idea di fornire una pista da corsa modulare sia ottima.
Volevo fare un'analisi approfondita della modularità della scheda e Flamme Rouge ha presentato l'occasione perfetta per farlo. Ma come possiamo calcolare quante varianti di tabellone sono offerte da un gioco del genere? È ora di introdurre uno strumento molto potente per aggiungere variabilità.
L’approccio combinatorio
Quando l'ordine è importante, come nel tracciare la pista, combinare pochi elementi (o items) è un modo semplice per offrire un gran numero di possibilità. Con 2-3 oggetti, forse non così tanto, ma se il numero di articoli è un po' più grande, i numeri crescono molto velocemente!
Così velocemente che i termini usati non sono di crescita esponenziale, ma piuttosto di esplosione combinatoria!
Se riordini semplicemente gli elementi, la crescita della combinazione possibile è la seguente: Se hai 5 elementi e vuoi scegliere un ordine, hai 5 scelte per il primo elemento da scegliere. Quindi hai 4 elementi, poi 3, poi 2 e infine uno.
Lo schema qui è facile da vedere. Per calcolare qualsiasi numero di combinazione prendi il numero totale N e lo moltiplichi per N-1, N-2,… fino a quando non ti rimane solo un elemento.
1 elemento = 1 possibile modo di ordinare
2 elementi = 2×1 – o 2 possibili modi di ordinare gli elementi
3 elementi = 3x2x1 – o 6 possibili modi di ordinare gli elementi
4 elementi = 4x3x2x1 – o 24 possibili modi di ordinare gli elementi
5 elementi = 5x4x3x2x1 – o 120 possibili modi di ordinare gli elementi
6 elementi = … – 720 possibili modi di ordinare gli elementi
7 elementi = 5040 possibili modi di ordinare gli elementi
8 elementi = 40320 possibili modi di ordinare gli elementi
9 elementi = 362 880
10 elementi = 3 628 800
eccetera…
In termini matematici, si chiama fattoriale e di solito si scrive con un punto esclamativo. Quindi puoi scrivere 10! = 3 628 800.
In qualità di programmatore, la velocità con cui un problema aumenta di dimensioni man mano che aggiungiamo elementi da considerare è chiamata complessità. Solo per il gusto di farlo, ecco un grafico che confronta diverse complessità per problemi che trattano da 1 a 100 elementi (l'asse X) e quanto velocemente cresce la loro complessità (asse Y).
Solo per il gusto di farlo, poniamo di avere alcune biglie...
La crescita di complessità più lenta possibile per un problema è l’assenza di crescita, che si chiama complessità costante.
Un buon esempio di un problema di complessità costante sarebbe la determinazione del peso totale di un gruppo di biglie. Poiché puoi pesare tutte le biglie contemporaneamente, la complessità è indipendente dal numero di biglie. La ponderazione 1 o 100 di esse consiste nello stesso numero di operazioni.
Nel discorso sulla crescita della complessità (chiamato Big-O in informatica), questo è indicato da O (1), mostrato nel grafico sopra dalla linea piatta in basso.
Un po’ più complesso
Un problema che mostra una crescita lineare, proporzionale al numero di biglie che hai, potrebbe essere quello di determinare quante biglie di un certo tipo hai.
Per questo, devi guardarli tutti, ma solo una volta. Il grafico mostra questo come complessità O (n) in verde nella parte inferiore del grafico. Da questo supponiamo che sia circa il doppio del tempo per elaborare 20 biglie che per elaborarne molte 10.
Da lì la complessità cresce molto più velocemente
Se le biglie fossero di colori diversi e volessi ordinarle in base alla loro tonalità di blu, ti troveresti di fronte a una complessità O(n log n) o addirittura O( n2 ).
Questa volta, la complessità dipende in realtà da come affronti il problema: Sapere come ordinare le cose in modo efficiente può farti risparmiare un'enorme quantità di tempo!
Se il tuo problema cresce in complessità fino alla potenza di 2, il numero di operazioni in take è proporzionale al quadrato del numero di elementi che hai. L'ordinamento di 20 biglie richiederà quattro volte più tempo dell'ordinamento di 10. Ma l'ordinamento di 100 biglie richiederà 100 volte più tempo dell'ordinamento di esse. Diventa quindi importante Iniziare rapidamente a cercare un modo per migliorare il tuo approccio!
Infine, se hai un problema di complessità fattoriale, l'estrema sinistra in blu sul grafico, puoi vedere che aumenta in modo follemente veloce, quindi di solito fai del tuo meglio per evitare questo tipo di problema. Ma è esattamente il caso che abbiamo nella nostra situazione di pista combinatoria: contare il diverso numero di modi di ordinare validi!
Non dimentichiamo che nel nostro caso i grandi numeri vanno bene, perché significano un gran numero di modi per creare diverse piste da corsa per il gioco! (È solo un peccato per me che sto cercando di analizzarlo!) Quindi questo è per la teoria, ma una serie di cose influenza il modo in cui la reale complessità emerge in un'analisi reale: se usiamo solo un sottoinsieme dei pezzi, se alcuni pezzi sono identici, o se il posizionamento dei pezzi ha dei vincoli, quelli sono tutti fattori che influiranno sul numero di combinazioni possibili e potrebbero aiutarci a risparmiare un po' di tempo!
Trovare il numero totale di piste possibili
Nel gioco base Flamme Rouge, usiamo sempre tutti i binari, ma ce ne sono 21... a doppia faccia! Questo offre un bel po' di possibilità.
Nella confezione ci sono 6 tracciati iniziali che il giocatore può provare. Ma puoi organizzare le tiles della pista come preferisci, fornendoti un bel po' di tracciati possibili! Ma quanti?
un re ogni anno convoca i suoi 10 feudatari che devono portargli 10 lingotti d'oro da un kilo ciascuno. un anno il re si accorge che qualcuno "allegerisce" i lingotti ma non sa chi è. quando dopo un anno i 10 sudditi tornano con i rispettivi 10 lingotti, il re si fa trovare con una bilancia e li minaccia: con una sola pesata sapò identificare il traditore! come fà?
un re ogni anno convoca i suoi 10 feudatari che devono portargli 10 lingotti d'oro da un kilo ciascuno. un anno il re si accorge che qualcuno "allegerisce" i lingotti ma non sa chi è. quando dopo un anno i 10 sudditi tornano con i rispettivi 10 lingotti, il re si fa trovare con una bilancia e li minaccia: con una sola pesata sapò identificare il traditore! come fà?
L'indovinello era in un episodio del Tenente Colombo... quello del club dei geni
Da non addetto ai lavori (grazie Goblin02 della dritta, laureato in archeologia orientale qui XD) ho trovato questa traduzione stimolante e molto interessante, specie per le ricadute sul game design di alcuni aspetti statistici di cui si parla di sopra.
Spero di portarvi al più presto altri episodi della serie, se avete apprezzato :p
Per scrivere un commento devi avere un account. Clicca qui per iscriverti o accedere al sito
La Tana dei Goblin protegge e condivide i contenuti del sito in base alla seguente licenza Creative Commons: Attribuzione - Non Commerciale - Condividi allo stesso modo, v.4.0. Leggi il testo sintetico, oppure il testo legale della licenza.
